点推定の求め方を詳しく解説！【例題あり】

「点推定という言葉を聞いたけど、何をするものなの？」
「実際にはどうやって使うの？」

このような疑問に対して、点推定の考え方から、具体的な求め方まで詳しく解説します。

点推定の考え方

そもそも、点推定とは何でしょうか？

点推定を使うと、例えば以下のことが分かります。

• 商品の中に含まれている添加物の量を測定して、商品全体の平均的な添加物の量や、ばらつきを予測する
• 大量生産している製品の抜き取り検査を行って、不良品の数から、製品全体の不良率を予測する
• 大きな金属板の一部を、顕微鏡で検査してキズの個数を数えて、金属板全体のキズの数を予測する

共通していることは、全体を調べることが困難なので、一部を抜き取って全体を予測するということです。

「一部のデータから全体を予測する」というのが点推定の考え方の本質です。

図で表すと以下のようになります。

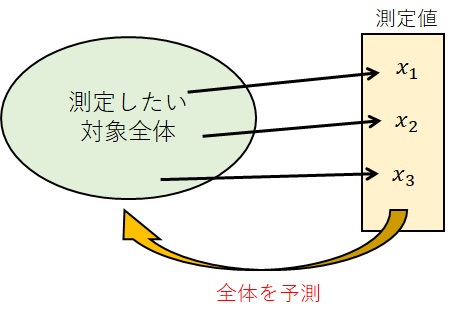
点推定を使うと、一部から全体を予測できるということを、イメージしていただけましたでしょうか？

では、具体的に点推定をどのようにして求めるのかを見ていきましょう。

点推定の求め方【正規分布・二項分布・ポアソン分布】

よく使われる分布として 3 つ(正規分布・二項分布・ポアソン分布)示します。

抜き取ったデータを \(x_1,x_2,\cdots,x_n\) として、データの平均値を \(\bar{x}\) とします。

分布	予測したい値	求め方
正規分布	平均	\(\bar{x}\)
正規分布	分散	\(\frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{x})^2\)
二項分布	平均	\(\bar{x}\)
ポアソン分布	平均	\(\bar{x}\)

実際のデータに対して、どのように使うのかを、例を見ながら学習しましょう。
以下では、正規分布と二項分布について解説します。

正規分布の点推定の求め方

例題の場合、正規分布に従っていると仮定して計算します。
平均と分散は、以下の値を計算して推定することができます。

分布	予測したい値	求め方
正規分布	平均	\(\bar{x}\)
正規分布	分散	\(\frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{x})^2\)

100 個の商品の添加物の量の平均は、表を参考にして、
\begin{align}
\bar{x}&=\frac{18+20+17+18+19}{5}\\
&=18.4
\end{align}
と計算できます。

分散を計算するときには、\(n=5\)ですので、
$$\frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{x})^2=1.3$$
となります。
式の具体的な計算方法は以下の記事を参考にしてください。

以上の計算から、

100 個の商品の添加物の量は、平均 18.4、分散 1.3

ということが分かります。

お気づきの方もいると思いますが、計算途中に「100」という数字は一度も登場していません。
つまり、商品全体が何個であろうが、点推定の結果は変わらないということです。

二項分布の点推定の求め方

この例のように、二者択一のものを扱うときには二項分布が使われます。

全体の比率は次のように求められます。

分布	予測したい値	求め方
二項分布	平均	\(\bar{x}\)

つまり、1000 個の商品全体の不良率はデータの平均 \(\bar{x}\) で求められます。
8 個のうち 2 個が不良品だったので、
$$\bar{x}=\frac{2}{8}=\frac{1}{4}$$
となります。

抜き取った商品の不良率が 1/4 で、1000 個の商品全体の不良率も 1/4 なので、感覚的に分かりやすいと思います。

まとめ

本記事では、点推定の考え方と求め方を紹介しました。

点推定とは「一部のデータから全体を予測する」ことです。

点推定の求め方として、正規分布・二項分布・ポアソン分布を例示しました。
どれもデータの平均を計算することで、全体の平均を求められるので、直感と合っています。

ぜひ点推定の求め方をマスターしてください。