こんにちは、マハルです。
この記事では、平均・分散・標準偏差といった統計の基礎を理解するための考え方をまとめています。
平均のイメージ
平均はデータの重心と考えるとわかりやすい
平均は日常生活でも使うので、知っている方も多いと思いますが、なんとなく理解したつもりになっていないでしょうか。
平均とは、データの「中心的な位置」を表します。
しかし、ひとことで「中心的な位置」といっても、あいまいで人によってとらえ方が違うと思います。
そのため、数直線を使って直感的にイメージできる方法を紹介します。
下図に数直線があります。左側が小さい値で、右に行くにつれて大きくなっていきます。そしてデータを黒い丸印で表しています。
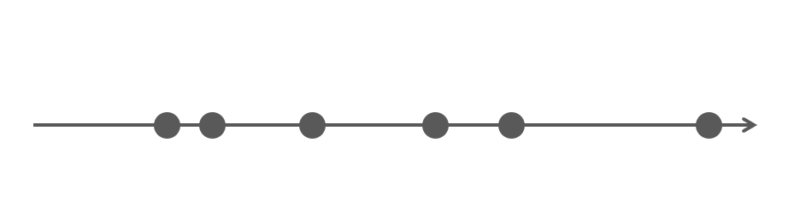
中心的な位置、つまり平均を求めていきましょう。まず、数直線を1本の棒として、手で持つことができると想像してください。データの黒い丸印がおもりです。
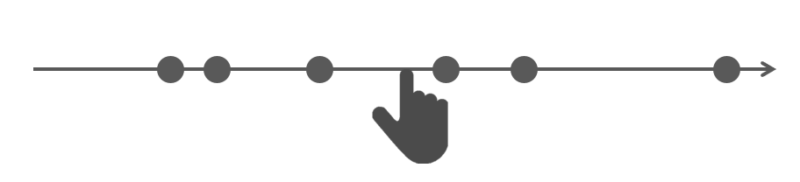
あなたはすごく力持ちで、この重りがついた棒を指1本で支えます。
左右の重りが釣り合う場所が1か所だけあって、その位置に指を置くとバランスを保って棒を支えることができます。
いわゆる重心とよばれる位置で、指1本で支えられる位置のことを平均といいます。
平均の計算方法
\(x_1, x_2, \cdots, x_n\)というように\(n\)個のデータがあるとします。平均は、データを全部足して、データの個数\(n\)で割ると計算できます。$$\bar{x}=\frac{1}{n} (x_1+x_2+\cdots+x_n)$$
たとえばお菓子が3つあって、値段がそれぞれ100円、120円、130円とします。
このときの平均値は、小数点第一位を四捨五入して、$$\bar{x}=\frac{1}{3} (100+120+130)=177$$となります。
発展:なぜデータの重心が平均なのか
データの重心が平均値と同じであることを、数式で説明します。
\(n\)個のデータを\(x_1, x_2, \cdots, x_n\)として、データの重心を\(\bar{x}\)とおきます。
重心とは、指1本でバランスをとれる点のことです。
つまり、つりあっている状態を式で書くと、$$(\bar{x}-x_1)+(\bar{x}-x_2)+\cdots+(\bar{x}-x_n)=0$$となります。
この式を変形すると、平均値の計算式、$$\bar{x}=\frac{1}{n} (x_1+x_2+\cdots+x_n)$$を導くことができます。
分散の意味と計算方法
分散の意味
分散とはデータのばらつき具合を表す指標です。
そもそもなぜ分散が必要かということですが、平均だけではうまくデータを表せないからです。
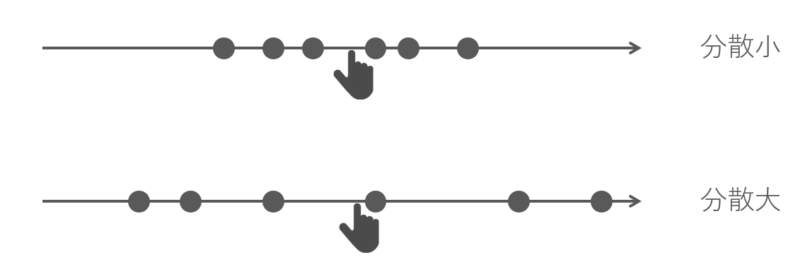
上の図は2種類のデータを表しています。
上と下どちらも平均は同じですが、明らかに見た印象が違います。
上のデータは平均の近くにかたまっているのに対して、下のデータは平均から大きく離れています。
データが平均からどのくらい離れているかというのを表すのが分散です。
上のデータは分散が小さく、下のデータは分散が大きいです。
分散の計算方法
分散は、平均からの差をとって2乗すると求めることができます。
\(n\)個のデータを\(x_1, x_2, \cdots, x_n\)として、データ平均を\(\bar{x}\)とすると、以下の式で書くことができます。
$$s^2=\frac{1}{n} \{(x_1-\bar{x})^2+(x_2-\bar{x})^2+\cdots+(x_n-\bar{x})^2\}$$
2乗にしている理由は、かっこの中がプラスにもマイナスにもなるからです。
プラスとマイナスが打ち消しあって、データのばらつき具合を計算できなくなるので、2乗がついています。
絶対値でもいいように思えますが、2乗にしておくと数学的な計算が楽になるので2乗が採用されています。
分散を計算するときは、次の節で紹介する式を使うのが楽なので、一旦とばします。
分散を楽に計算する方法
前節では、分散の式を紹介しました。
$$s^2=\frac{1}{n} \{(x_1-\bar{x})^2+(x_2-\bar{x})^2+\cdots+(x_n-\bar{x})^2\}$$
しかし、実際に計算するとき、すべてのデータについて平均値との差をとるのは、めんどうです。
そこで、分散の式を変形した以下の式を使って計算します。
$$s^2=\frac{1}{n} (x_1^2+x_2^2+\cdots+x_n^2)-\bar{x}^2$$
たとえば、3つのお菓子があって、値段がそれぞれ100円、120円、130円とします。平均は116.7円です。
先ほどの式に代入すると、分散を計算することができます。
$$s^2=\frac{1}{3} (100^2+120^2+130^2)-116.7^2=155.6$$
発展:分散の計算を楽にする式の証明
前節で紹介した、分散の計算を楽におこなうための式が、なぜ成り立つのかを証明します。
分散は、以下の式で定義されています。
$$s^2=\frac{1}{n} \{(x_1-\bar{x})^2+\cdots+(x_n-\bar{x})^2\}$$
この式を変形していきます。
\begin{align}
s^2&=\frac{1}{n} \{(x_1^2-2x_1\bar{x}+\bar{x}^2)+\cdots+(x_n^2-2x_n\bar{x}+\bar{x}^2)\}\\
&=\frac{1}{n} \{(x_1^2+\cdots+x_n^2)-2\bar{x}(x_1+\cdots+x_n)+n\bar{x}^2\}\\
&=\frac{1}{n} \{(x_1^2+\cdots+x_n^2)-2\bar{x}\times n\bar{x}+n\bar{x}^2\}\\
&=\frac{1}{n} \{(x_1^2+\cdots+x_n^2)-n\bar{x}^2\}\\
\end{align}
式変形の中身を説明すると、1行目はカッコの中を展開しています。
2行目から3行目の変形には、平均値の定義$$\bar{x}=\frac{1}{n} (x_1+x_2+\cdots+x_n)$$を使用しています。
よって、分散の定義式を変形することで、
$$s^2=\frac{1}{n} (x_1^2+x_2^2+\cdots+x_n^2)-\bar{x}^2$$
をみちびくことができました。
標準偏差を使う理由
分散の欠点と標準偏差の意味
分散をつかうとデータのばらつき具合を数値であらわすことができましたが、解釈が難しいという欠点があります。
分散の値だけでは、ばらつきが大きいのか小さいのか判断がつきません。分散の数値に意味を与えるために標準偏差というものがあります。
標準偏差は、分散の平方根で計算することができます。
\(n\)個のデータを\(x_1, x_2, \cdots, x_n\)として、データ平均を\(\bar{x}\)とすると、以下の式で書くことができます。
$$s=\sqrt{s^2}=\sqrt{\frac{1}{n} \{(x_1-\bar{x})^2+(x_2-\bar{x})^2+\cdots+(x_n-\bar{x})^2\}}$$
たとえば、3つのお菓子があって、値段が100円、120円、130円のとき、分散は155.6でした。ここで分散の単位に着目すると、データの2乗を取っているので、単位は円の2乗になっています。
円の2乗というのはまったく意味のない単位ですので、平方根を取って単位をそろえたのが標準偏差です。お菓子の値段の場合、標準偏差は12.5円です。
標準偏差の使いかた
まずここで、新しい用語を導入します。
標準偏差は\(\sigma\)(シグマ)と書くのが一般的なのでシグマを使って説明します。
「平均±標準偏差」の範囲のことを1シグマ区間と呼びます。一般的にkを正の整数として、「平均±k×標準偏差」の範囲のことをkシグマ区間と呼びます。
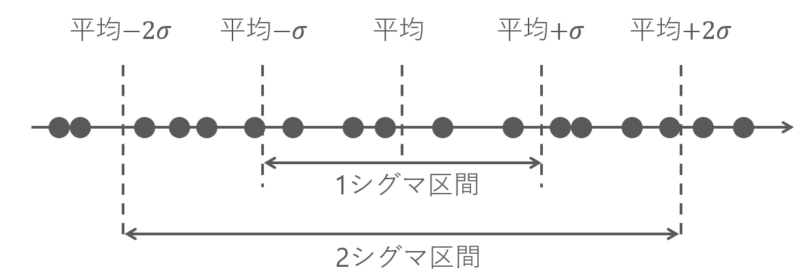
標準偏差は平均値プラスマイナス2シグマの中に全データの75%以上が入っていると解釈します。たとえばお菓子が1000個あって平均値が120円、標準偏差が10円であったとき、1000個のうち750個以上は100円から140円の間に入っています。
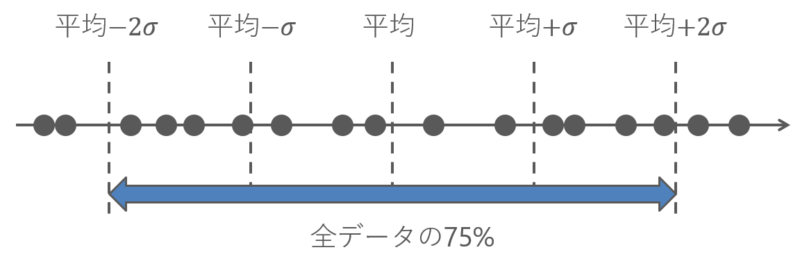
2シグマ区間に75%以上のデータが入っているというのは、チェビシェフの不等式から計算することができます。チェビシェフの不等式は数学的にかなり難しいので特に覚える必要はありません。
演習問題
問題
10人が体重を測定しました。
55kg、48kg、60kg、66kg、52kg、61kg、55kg、45kg、58kg、54kg
10人の体重の分散と標準偏差を計算してください。
解答・解説
分散を計算するためには、平均値が必要なので、まずは平均値を求めます。
平均値は以下の式を使います。
$$\bar{x}=\frac{1}{n} (x_1+x_2+\cdots+x_n)$$
10人の体重を代入して計算すると、
$$\bar{x}=\frac{1}{10} (55+48+60+66+52+61+55+45+58+54)=55.4$$
体重の平均値は55.4kgと求められました。
次に分散を求めます。
分散を計算するときは、以下の式を使います。
$$s^2=\frac{1}{n} (x_1^2+x_2^2+\cdots+x_n^2)-\bar{x}^2$$
10人の体重を代入して計算すると、
$$s^2=\frac{1}{10} (55^2+48^2+60^2+66^2+52^2+61^2+55^2+45^2+58^2+54^2)-55.4^2=34.84$$
体重の分散は34.84と求められました。
最後に標準偏差を計算します。標準偏差は分散の平方根なので、
$$s=\sqrt{s^2}=\sqrt{34.84}=5.9$$
よって、体重の標準偏差は5.9kgです。
まとめ
- 平均値はデータの重心
- 平均値を計算するときは、全部のデータを足してから、データ個数で割る
- 分散はデータのばらつき具合を数値で表したもの
- 分散が大きいほどデータのばらつき具合が大きい
- 標準偏差は分散の平方根
- 標準偏差は元データと同じ単位をもっているので、データのばらつきを視覚的に表すことが可能


