【不偏分散】ｎ－１で割って求める理由は？真の分散を偏りなく推定できるから

不偏分散を初めて習うときに必ず疑問に思うのが、

「なぜ n-1で割るのか」

ということでしょう。
本記事では、不偏分散はどのように使われるのかを解説して、n-1 で割る理由を直感的に理解できるようにします。

不偏分散の求め方と利用場面
不偏分散がn-1で割られる理由
まとめ
1. 参考文献

不偏分散の求め方と利用場面

初めに不偏分散の求め方を確認します。
不偏分散とは、複数のデータがあるとき、それが平均からどのくらいバラツキがあるのかを表す指標です。

データが $x_1,x_2,\cdots,x_n$ の n 個あるとき、不偏分散は以下のように定義されます。
$$s^2=\frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{x})^2$$
ここで $\bar{x}$ は n 個のデータの平均値を表します。

以下では、「なぜ n ではなく n-1 で割るのか」ということに焦点を当てて解説します。

n-1 で割る理由を理解するためには、「不偏分散を何のために計算するのか」ということを知っている必要があります。

本節では不偏分散を計算する理由を説明し、次節で n-1 で割る理由を解説します。

さて、不偏分散を計算する理由を、下図を使いながら見ていきましょう。

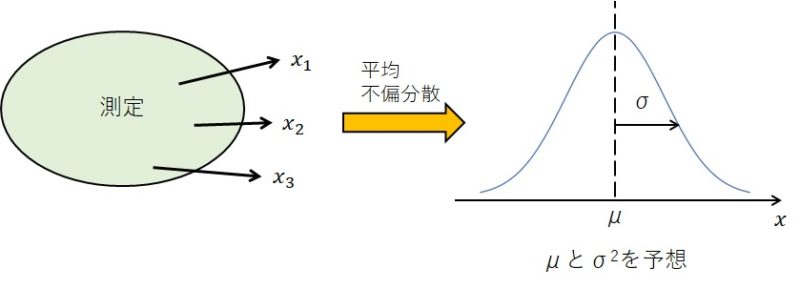
例えば、長さ、電流、温度等、何かを繰り返し測定してデータを集めることを考えます。

この測定したいものが、平均 $\mu$、分散 $\sigma^2$ の正規分布 $N(\mu,\sigma^2)$に従っているとします。

私たちは真の平均 $\mu$ や分散 $\sigma^2$ を知ることはできません。
測定を行う目的は、得られたデータから平均 $\mu$ や分散 $\sigma^2$ を予想することです。

ここで、データから不偏分散を計算することによって、真の分散 $\sigma^2$ を推定することができるのです。

不偏分散を使うことによって真の分散 $\sigma^2$ を精度よく推定できることは数学的に証明されており、これが不偏分散を計算する理由になっています。

(「精度よく推定」とあいまいな表現を使っていますが、推定について数学的に考察すると非常に難解になってしまうので、とりあえず「不偏分散で真の分散を推定できる」ということを知っていれば差し支えありません。)

不偏分散がn-1で割られる理由

前節では不偏分散を計算する理由を見てみました。
本題の n-1 で割られる理由を見ていきます。

不偏分散が n-1 で割られる理由を一言で説明すると、次のようになります。

「不偏分散の期待値が真の分散になるから($E[s^2]=\sigma^2)$」

($E[s^2]$ は、不偏分散 $s^2$ の期待値という意味です。)

教科書には上の式だけ書かれていることもありますが、多くの方は、この表現だけではピンと来ないと思います。

先ほどと似たような例を用いて、意味を丁寧に解説していきます。

例えば、測定して求めたいものが、平均 5、分散 0.2 の正規分布に従うとします。
(繰り返しになりますが、私たちは真の平均 5 と分散 0.2 が分からないので、測定によってこれらの値を推定します。)

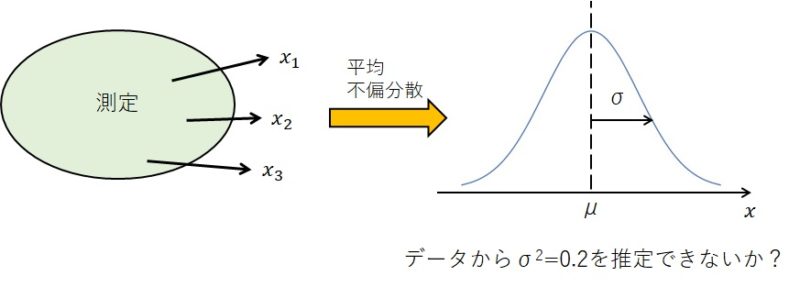
上図のように 3 個のデータを取って不偏分散
$$s^2=\frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{x})^2$$
を計算したところ、$s^2=0.18$となりました。(0.18は筆者が適当に決めました)

私たちがデータから分かるのは、不偏分散が 0.18 となったという事実だけで、真の分散が 0.2 であるとは分かっていません。

そこで、
「本当に真の分散は 0.18 なのかな？」
と疑問に思って、もう一度測定を 3 回行います。

すると、$s^2=0.21$となりました。
不偏分散の 2 回の平均値 $(0.18+0.21)/2=0.195$ は先ほどよりも真の分散 0.2 に近づきました。

このように、

繰り返し測定して 3 回データを取る
得られたデータから不偏分散を計算する
もう一度繰り返し測定して 3 回データを取る
得られたデータから不偏分散を計算する

という作業を何回も行います。
すると、「計算された不偏分散の平均値は、真の分散 0.2 になる」というのが、冒頭で述べた

「不偏分散の期待値が真の分散になる($E[s^2]=\sigma^2)$」

という意味です。
不偏分散の「不偏」というのは、「偏りがない」という意味で、「期待値は真の分散からずれていない」ということを表しています。
理解していただけましたでしょうか？

なお、不偏分散を使わずに、n で割った分散(標本分散と呼ばれることが多いです)
$$v^2=\frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})^2$$
を使ってしまうと、標本分散の期待値は
$$E[v^2]=\frac{n-1}{n}\sigma^2$$
となります。

先ほどと同じように測定を 3 回行って標本分散を計算する、ということを繰り返すと、平均値は
$$\frac{3-1}{3}\times 0.2=0.133$$
に近づいてしまい、真の分散 0.2 を正しく推定できないことになってしまいます。

n が非常に大きいときには (n-1)/n の値は 1 に近づくので、標本分散を用いても不偏分散を用いてもあまり差はありません。

しかし、n が小さいときに標本分散を使って真の分散を推定しようとすると、真の分散から大きくずれてしまうので注意が必要です。