ヒストグラムの標準偏差の求め方【5つの手順で求める】

ヒストグラムを使って標準偏差が求められることをご存知ですか？
「標準偏差」と聞くと難しそうに感じますが、実際には高度な計算は要求されません。

本記事では、初めて標準偏差を計算する方でも理解できるように、詳しく解説します。

ヒストグラムの標準偏差とは？

次の例題を使って説明します。

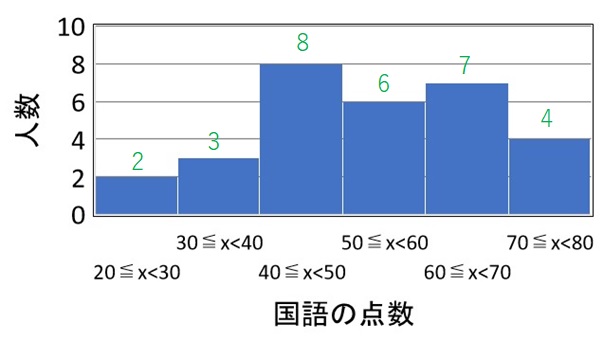
ヒストグラムとは、上のグラフのように、「1 つ 1 つの区間にデータが何個あるか」を表したものです。

続いて、標準偏差についてです。

標準偏差とは、「データが、平均からどのくらい離れているか」を表した数値です。
例題では、平均は下記の位置にあります。

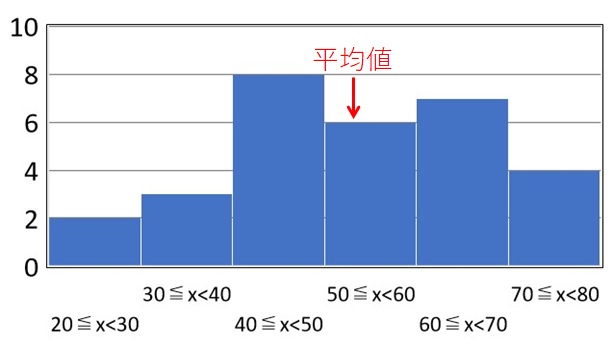
平均値から離れたところにデータが多くあると、標準偏差は大きくなります。
反対に、平均値付近にデータが集まっていると、標準偏差は小さくなります。

このように、標準偏差を見ることで、データの集まり具合を判断することができます。

計算方法の具体的な手順

本節では、ヒストグラムを使って標準偏差を計算する方法を順を追って解説します。
先ほどと同じ例題を使用しますので、以下に再掲します。

標準偏差を計算するときに使う式

これから行う計算手順の意味を知っていただくために、標準偏差の求め方を示します。
データが\(x_1, x_2, \cdots , x_n\)の n 個あるとき、標準偏差は以下の式のように表されます。
\begin{align}
s&=\sqrt{\frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})^2}\\
&=\sqrt{\frac{1}{n}\sum_{i=1}^n x_i^2-\frac{1}{n^2}\left(\sum_{i=1}^n x_i\right)^2}
\end{align}
1 行目の式は、標準偏差の定義式です。\(\bar{x}\) はデータの平均を表します。
ヒストグラムから計算するときには 1 行目の式は使いにくいので、2 行目の式を使うことになります。

2 行目の式を使って標準偏差を求めるためには、
$$\sum_{i=1}^n x_i^2, \sum_{i=1}^n x_i$$
の 2 つの値を計算する必要があります。
つまり、(個々のデータの 2 乗の和)、および、(個々のデータの和)の 2 つを求めます。

言葉だけでは分かりにくいと思いますので、データを見ながら解いてみましょう。

手順1 階級値を計算する

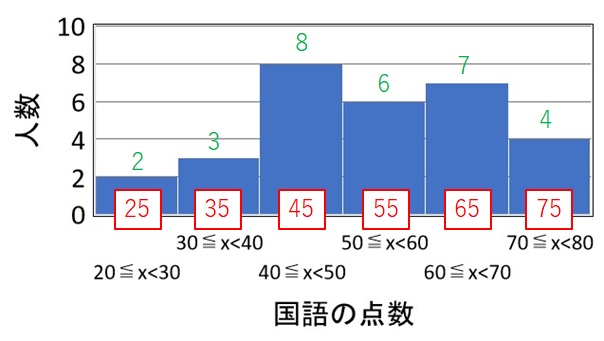
まずは、各区間のデータを知る必要がありますので、階級値(=区間の中央の値)を求めます。

結果は、上図の赤枠の数値になります。

手順2 階級値×度数を計算する

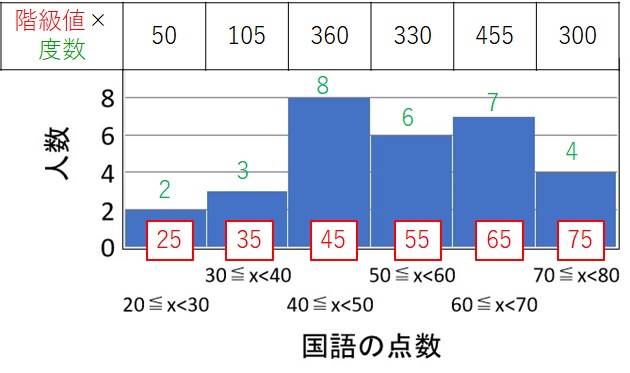
度数とは、データの数のことで、縦軸の値が度数になります。

手順 1 で求めた階級値(赤色)と度数(緑色)の数字をかけて、表の中に書きました。
この数字にはどのような意味があるのかと言いますと、

1. 「20 ≦ x < 30」だけでは一人一人の生徒が何点取ったのか分からないので、とりあえず全員 25 点取ったことにする。
2. 「20 ≦ x < 30」を取った生徒は 2 人いるので、2 人の合計点数を \(25 × 2 = 50\) (点)とする

ということです。
これで、各区間の生徒の合計点数を知ることができます。

手順3 (階級値の 2 乗)×度数を計算する

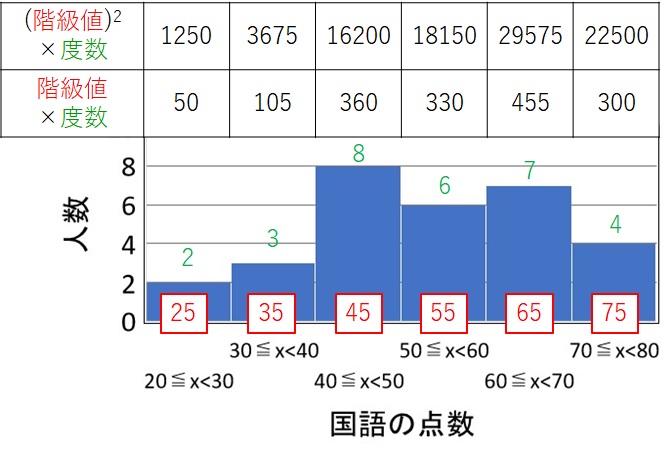
手順 1 で求めた階級値(赤色)を 2 乗して度数(緑色)をかけます。
この計算結果に深い意味はなく、標準偏差を計算するためだけに使います。

手順4 求めた値を合計する

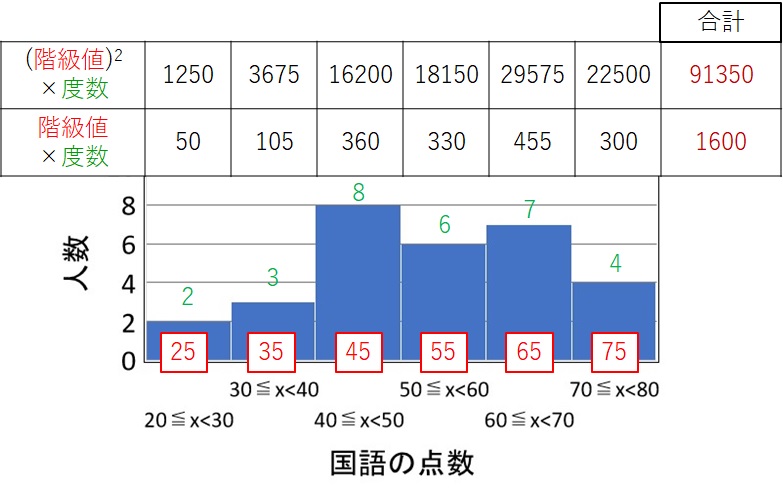
手順 2 と手順 3 で求めた値を合計して、表の中に書いています。
ここで求められた合計を次の手順で使うことになります。

手順5 標準偏差の式に代入する

最後に、標準偏差を求める計算式に代入します。

標準偏差は以下のように計算されるのでした。
$$s=\sqrt{\frac{1}{n}\sum_{i=1}^n x_i^2-\frac{1}{n^2}\left(\sum_{i=1}^n x_i\right)^2}$$

この式で、\(\sum_{i=1}^n x_i\)と、\(\sum_{i=1}^n x_i^2\)は手順 4 で求めた値を使います。
\begin{align}
\sum_{i=1}^n x_i&=1600\\
\sum_{i=1}^n x_i^2&=91350\\
\end{align}
生徒は全員で 30 人ですので、
\begin{align}
s&=\sqrt{\frac{1}{n}\sum_{i=1}^n x_i^2-\frac{1}{n^2}\left(\sum_{i=1}^n x_i\right)^2}\\
&=\sqrt{\frac{1}{30}\times 91350-\frac{1}{30^2}\times 1600^2}\\
&=14.2
\end{align}
よって、標準偏差が 14.2 点と求められました。

まとめ

本記事では、ヒストグラムから標準偏差を求める手順を解説しました。

少し計算する量が多いですが、上記の 5 つの手順に従えば確実に計算できますので、ぜひ電卓を持って計算してみましょう。