データ分析や機械学習では、「正規化」「標準化」はよく使われます。
本記事では、それらの手法を解説し、それぞれの適用シーンやメリット・デメリットについて掘り下げていきます。
正規化とは?
正規化は、データのスケールを統一する手法です。
具体的には、データを0~1の範囲におさめます。
データの範囲を0~1の範囲におさめることで、たとえば温度、距離、重量など、ことなる単位やスケールをもつデータの大きさをそろえられます。
正規化は、以下の式で計算できます。
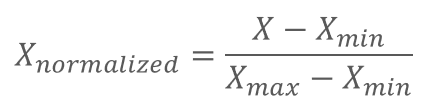
具体例をとおして、計算方法を見てみましょう。
ある店舗の1週間の売上データが、以下のように記録されています。
このデータを正規化してください。
| 曜日 | 売上(万円) |
|---|---|
| 月曜日 | 50 |
| 火曜日 | 30 |
| 水曜日 | 70 |
| 木曜日 | 90 |
| 金曜日 | 100 |
正規化するためには、まずデータの最小値と最大値をもとめます。
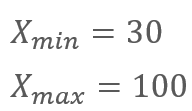
最小値は、火曜日の30万円、最大値は、金曜日の100万円です。
あとは公式にあてはめると計算できます。ためしに月曜日のデータを正規化してみます。

計算すると、0.286になりました。
そのほかの曜日も同じように計算します。
| 曜日 | 売上(万円) | 正規化後の値 |
|---|---|---|
| 月曜日 | 50 | 0.286 |
| 火曜日 | 30 | 0 |
| 水曜日 | 70 | 0.571 |
| 木曜日 | 90 | 0.857 |
| 金曜日 | 100 | 1 |
正規化すると、すべてのデータが0と1の間にあることがわかります。
また、最小値は0、最大値は1になります。
標準化とは?
標準化は、データを平均0、標準偏差1に変換する手法です。
標準偏差とは、データのばらつきを表すものです。
この変換をおこなう理由は、きれいな分布でデータを扱うほうが便利になるからです。
標準化は、各データから平均を引いて、その値を標準偏差で割ることでもとめられます。
標準化したデータは、Z-scoreともよばれます。
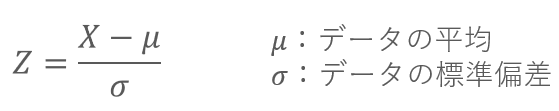
具体例をつかって、標準化を計算してみましょう。
あるクラスの5人の学生が受けたテストの点数があります。
このデータを標準化してください。
| 学生 | 点数 |
|---|---|
| Aさん | 50 |
| Bさん | 60 |
| Cさん | 70 |
| Dさん | 80 |
| Eさん | 90 |
標準化の方法は少し大変です。
まずは点数の平均を計算します。
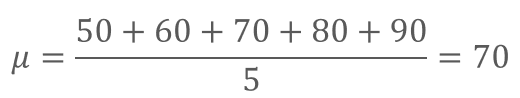
平均点は70点でした。
標準偏差は次の式で計算することができます。
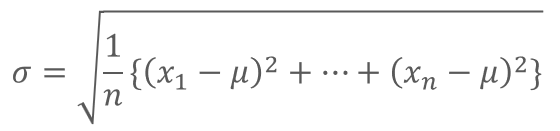
具体的な計算方法は、以下の記事で解説しています。
がんばって計算すると、標準偏差は14.14になります。
平均と標準偏差がわかったので、Aさんの点数を標準化してみます。
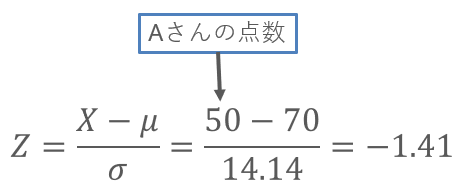
標準化の公式にあてはめると、-1.41となりました。
おなじようにして、残りの学生も計算してみましょう。
| 学生 | 点数 | Z-score |
|---|---|---|
| Aさん | 50 | -1.41 |
| Bさん | 60 | -0.71 |
| Cさん | 70 | 0 |
| Dさん | 80 | 0.71 |
| Eさん | 90 | 1.41 |
点数が平均点の70よりも低い場合はマイナス、70よりも高い場合はプラスになります。
また、平均から離れるほど、Z-scoreは絶対値が大きくなっていきます。
正規化と標準化のちがいを可視化してみる
もういちど、正規化と標準化をおさらいします。
- 正規化:データを0~1の範囲におさめる
- 標準化:データを平均0、標準偏差1に変換する
これらの違いを可視化してみましょう。
そのために、サイコロを1000回ふって、そのデータに対して、正規化と標準化をおこなってみます。
コンピュータでサイコロを1000回ふって、出た目の回数を記録したものを示します。
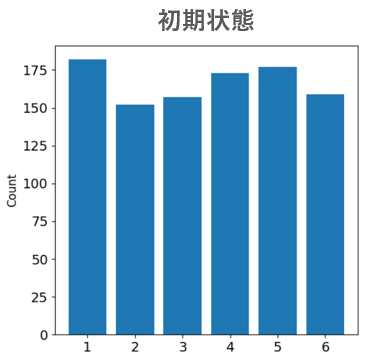
このデータに対して、正規化と標準化を計算してみました。
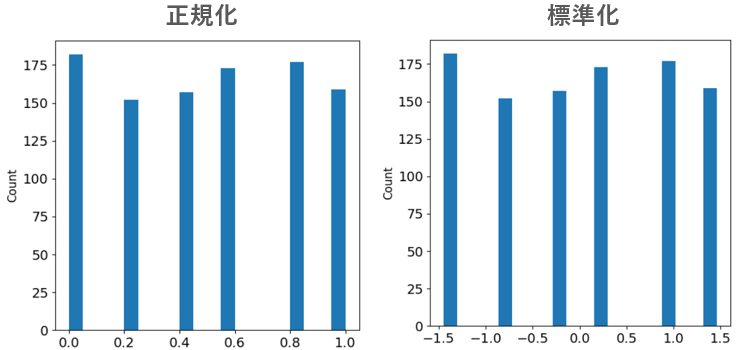
左が正規化、右が標準化の結果です。
まず、正規化も標準化も分布の形状は変わりません。
なぜなら、どちらも線形変換(平行移動とスケーリング)をしただけで、形状や相対的な高さは変わらないからです。
しかし、横軸に注目すると違いがあります。
正規化は、データを0~1におさまっていることがわかります。
標準化は平均0を中心とした分布となっています。
このように、正規化と標準化は分布の形状を変えずに、データの値を変換します。
まとめ
この記事では正規化と標準化のちがいを掘り下げました。
- 正規化:データを0~1の範囲におさめる
- 標準化:データを平均0、標準偏差1に変換する
変換の方法はそれぞれ公式があるので、それにあてはめると計算できます。
どちらも分布の形状は変えませんが、データの値そのものを変えることで、さまざまな機械学習モデルで計算しやすくすることができます。



