はじめに
確率を学ぶと、「条件付き確率」という言葉が登場します。
その名の通り、「ある条件が成り立ったときの確率」を表します。
しかし、条件付き確率は計算式がすぐには理解しづらく、よく分からずに計算してしまっている方も多いと思います。
この記事では、具体例を用いて条件付き確率の計算式の意味を解説していきます。
条件付き確率の具体例
ある工場では、2 台の機械を使ってクッキーを製造している。
この機械では一定の割合でクッキーの成形に失敗し、形が崩れて不良品となってしまう。
機械 A では不良品が 3 %、機械 B では不良品が 5 %となることが分かっている。
作られたクッキーを抜き取り検査したところ、不良品であった。
このクッキーが機械 A で作られた確率を求めよ。
ただし、機械 A と機械 B では同じ枚数のクッキーを製造している。
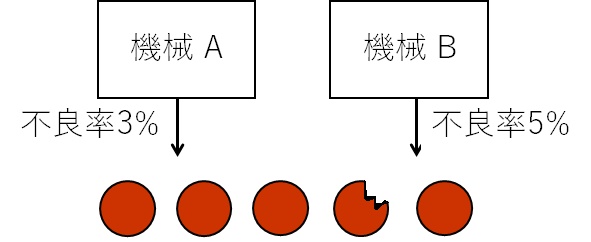
チョコレートクッキーをイメージして図を作成しました。
さて、不良品が見つかったときに、そのクッキーが機械 A から作られた確率を求めてみましょう。
ここでは条件付き確率の式を使わずに、直感的に分かりやすいように計算してみます。
例えば、機械 A で 100 枚、機械 B で 100 枚のクッキーを作ったと考えます。
すると、平均的に機械 A で作ったクッキーには不良品が 5 枚、機械 B で作ったクッキーには不良品が 8 枚できることになります。
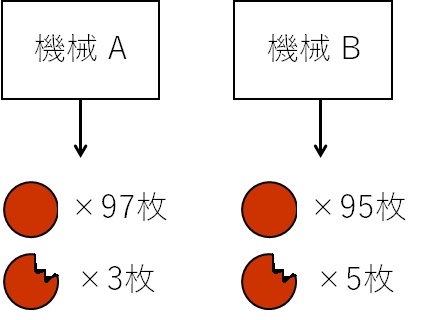
上の図のような状況です。
図を見てわかるように、クッキーは合計で 200 枚あり、不良品は 8 枚あります。
不良品であることが分かっているときに、そのクッキーが機械 A で作られた確率は、不良品 8 枚のうち 3 枚ですので、
$$P(機械 A | 不良品)=\displaystyle \frac{3}{8}$$
となります。
式の中の縦棒は条件を表す記号(「ギブン(Given)」と読みます ) で、縦棒の右側が条件となります。
つまり、この式の意味は、
「不良品という条件の下で、機械 A である確率は \(\displaystyle \frac{3}{8}\) である」
ということです。
この式から、条件付き確率の定義式がどのような意味を持っているのか考えましょう。
条件付き確率の式を変形すると、
\begin{align}P(機械 A | 不良品)&=\displaystyle \frac{3}{8}\\
&=\frac{\frac{3}{200}}{\frac{8}{200}}\\
&=\frac{P(機械A \cap 不良品)}{P(不良品)}
\end{align}
単に分子と分母を標本数(機械 A と機械 B で作ったクッキーの合計 200 枚)で割っただけです。
変形した最後の式が、条件付き確率の式として教科書に出てくる式となります。
記号がたくさん登場するので圧倒されますが、
「不良品全部の数を分母として、そのうち機械 A で作られた数を分子とする」
ということを述べているだけです。
おわりに
いかがでしたでしょうか。
条件付き確率の式は複雑に見えますが、条件が与えられたとき、その条件を分母として計算しているだけの式になります。
初めのうちは公式に当てはめるのではなく、上で見たように順を追って考えていくと理解しやすくなります。
筆者も条件付き確率の公式を理解するのには時間がかかりましたが、具体的な数値を当てはめていくことで、公式の意味を理解することができました。
ぜひ、紙と鉛筆を使って式の意味を確かめてみてください。


