【統計】独立とは

はじめに

確率や統計の分野では、独立という言葉がよく出てきます。
日常では「何かに依存しないこと」を独立と捉えているように思います。

確率統計でもニュアンスは同じです。
ただし、数学という学問の性質上、日常で使う言葉と違って意味をはっきりさせなければなりません。

この記事では確率統計の分野で使われる独立の意味がよく分からない、という方へ向けて、独立とは何か、を解説していきます。

例題で考える独立の意味

例題を使って独立の意味を見ていきます。

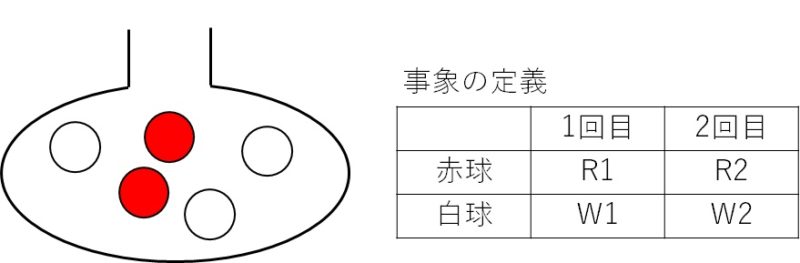
この問題を解くために、上図のように事象を定めます。(RはRed、WはWhiteの意味)
例えば1回目に赤球を取り出したということをR1と書くことにします。

すると、1回目に赤球、2回目に白球を取り出す確率は、

$$P(R1 \cap W2)$$

と書くことができます。

1回目に何色の球を取り出そうが、2回目に白球を取り出す確率は変わりません。
つまり、確率は、

\begin{align}
P(R1 \cap W2)&=P(R1) \times P(W2)\\
&=\frac{2}{5} \times \frac{3}{5}\\
&=\frac{6}{25}
\end{align}

この例のように、事象W2が事象R1の影響を受けないことを独立と呼びます。

もう少し詳しく述べると、2回目に球を取り出す時点で、1回目に赤球を取り出したことは分かっていますが、その情報は2回目に白球を取り出す確率に影響を与えないということです。

2つの事象R1とW2が独立であるとき、上の計算式で示しているように、次の関係が成り立ちます。

$$P(R1 \cap W2)=P(R1) \times P(W2)$$

(注：独立を定義するときに条件つき確率を使っている文献も多いですが、ここでは話を分かりやすくするために条件つき確率は使用しません。)

式を言葉で説明すると、
「1回目に赤球を取り出す確率と、2回目に白球を取り出す確率は独立だから、掛け算で求めることができる」

ポイントは、独立のときは確率を掛け算することができるということです。

独立でない場合と比較して、詳しく見ていきましょう。

独立でない場合

先ほどの例題を少し変更します。

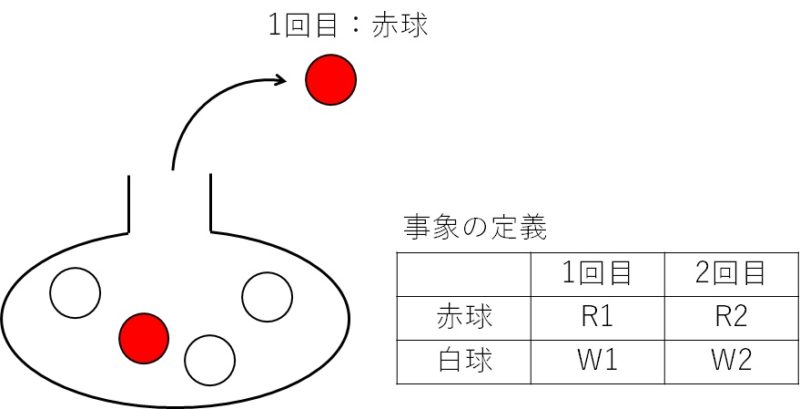
1回目に取り出した球を元に戻さないとき、2回目に白球を取り出す確率は1回目に取り出した球の色の影響を受けます。
このことを式で確認してみましょう。

1回目に赤球、2回目に白球を取り出す確率は、

\begin{align}
P(R1 \cap W2)&=\frac{2}{5} \times \frac{3}{4}\\
&=\frac{3}{10}
\end{align}

1回目で赤球を取り出してしまったので、2回目に取り出すときには、つぼの中の球の数は4になっており、その4つの中から白球を取り出す確率は\( \displaystyle \frac{3}{4}\)となります。

ここで、独立であることを示す関係式が成り立つか確認してみましょう。

1回目に赤球を取り出す確率は、
$$P(R1) = \frac{2}{5}$$

2回目に白球を取り出す確率は次のように求められます。
1回目に赤球、2回目に白球を取り出す場合と、1回目に白球、2回目に白球を取り出す場合があるので、
\begin{align}
P(W2)&=\frac{2}{5} \times \frac{3}{4} + \frac{3}{5} \times \frac{2}{4}\\
&=\frac{3}{5}
\end{align}

今までの3つの式をまとめると、

$$P(R1 \cap W2) = \frac{3}{10} , P(R1) = \frac{2}{5} , P(W2) = \frac{3}{5}$$

となっており、

$$P(R1 \cap W2) \neq P(R1) \times P(W2)$$

つまり、独立でないときには掛け算で計算できないことが分かります。

まとめ

今回のつぼから球を取り出す例題でまとめると、

独立とは、1回目で球を取り出すという事象が、2回目で球を取り出す確率に影響を与えないこと

と言うことができます。
また、独立であるときには次の関係式が成り立ちます。

$$P(R1 \cap W2)=P(R1) \times P(W2)$$

問題設定が難しくて独立かどうかをすぐに判断できないときには、この式を使って判断する方が確実です。

以上、確率統計の分野における独立の説明でした。