
ベイズの定理って何?
記号ばっかりで覚えられる気がしない…
ベイズの定理を見たとき、式の複雑さに圧倒されていませんか?
本記事では、ベイズの定理の意味を図で詳しく解説します。
はじめにベイズの定理の証明を示します。
証明では数式が多くなってしまいますので、
具体例の項目で直感的にイメージできることを目指します。
図で理解するベイズの定理の証明
ベイズの定理とは、
原因→結果 の確率
がわかっているときに、
結果→原因 の確率
を求める定理です。
つまり、実験や観察で結果が得られたとき、原因は何かということを知ることができます。
図を使って詳しく見てみましょう。
\(B\) という結果が得られました。
原因として \(A_1\)、\(A_2\) の2つがあったとします。
このとき、原因と結果の関係は下図のようになります。
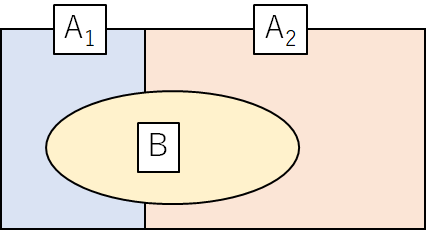
\(A_1\) が原因で結果 \(B\) が生じた確率は、条件つき確率より、
$$P(B|A_1)=\frac{P(A_1\cap B)}{P(A_1)}$$
これは原因→結果の確率です。
反対に、結果 \(B\) がわかっているときに、\(A_1\) が原因である確率は、
$$P(A_1|B)=\frac{P(A_1\cap B)}{P(B)}$$
この式は結果→原因を表す確率となります。
2つの式から\(P(A_1\cap B)\)を消去すると、
\begin{align}
P(A_1|B)P(B)&=P(B|A_1)P(A_1)\\
P(A_1|B)&=\frac{P(B|A_1)P(A_1)}{P(B)}
\end{align}
最後の式をよく見てみると、原因→結果の確率から、結果→原因の確率を求めていることがわかります。
この式を使って計算できそうですが、実際には結果が生じた確率 \(P(B)\) を計算することは困難です。
そこで、\(P(B)\) を計算するために、原因と結果の関係図を再び見てみます。
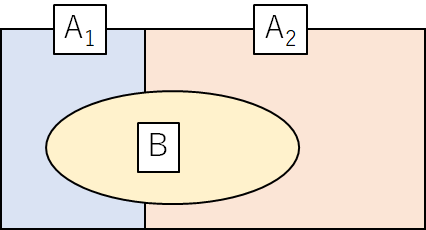
結果 \(B\) は、\(A_1\) か \(A_2\) のどちらかに属しているので、
\begin{align}
P(B)&=P(A_1\cap B)+P(A_2\cap B)\\
&=P(B|A_1)P(A_1)+P(B|A_2)P(A_2)
\end{align}
よって、
\begin{align}
P(A_1|B)&=\frac{P(B|A_1)P(A_1)}{P(B)}\\
&=\frac{P(B|A_1)P(A_1)}{P(B|A_1)P(A_1)+P(B|A_2)P(A_2)}
\end{align}
これが「ベイズの定理」と呼ばれています。
証明の流れをまとめると、
- 原因→結果の確率と、結果→原因の確率を求める
- 共通する部分を消去して、1つにまとめる
- 結果の確率を、原因 \(A_1\) の部分と、原因 \(A_2\) の部分に分ける
となっています。
今までの証明の流れは、記号ばっかりで抽象的でしたので、具体例を使いながらベイズの定理の意味を再確認してみましょう。
具体例で学ぶベイズの定理の意味
杉原さんのお店では、工場 \(A_1\) から仕入れたお菓子と、工場 \(A_2\) から仕入れたお菓子を販売している。
販売しているお菓子の内訳は、工場 \(A_1\) からが 30%、工場 \(A_2\) からが 70% である。
しかし、仕入れるお菓子の一部には不良品が混ざっている。
工場 \(A_1\) のお菓子は 5% が不良品で、工場 \(A_2\) のお菓子は 3% が不良品である。
お店のお菓子に不良品が見つかったとき、それが工場 \(A_1\) から仕入れたお菓子である確率を求めよ。
例題を用いて、ベイズの定理をもう一度追ってみましょう。
不良品を \(B\) と書くと、例題の条件は以下のようになります。
\begin{align}
P(A_1)&=0.3\\
P(A_2)&=0.7\\
P(B|A_1)&=0.05\\
P(B|A_2)&=0.03\\
\end{align}
条件つき確率を \(P(B|A_1)\) と書くことに注意してください。
\(B\) と \(A_1\) を反対にしてしまうと別物になってしまいます。
さて、数式だけでは味気ないので、条件を図であらわしてみました。
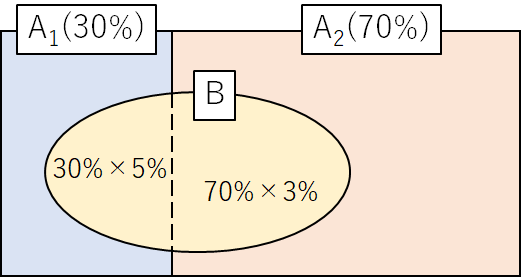
工場 \(A_1\) のお菓子の不良率は 5%、工場 \(A_2\) のお菓子の不良率は 3% ですので、
図のように共通部分の確率を計算することができます。
図を見ながら、不良品 \(B\) が見つかったときに、工場 \(A_1\) から仕入れた確率 \(P(A_1|B)\) を求めてみます。
ベイズの定理は何をあらわしているかというと、不良品 \(B\) 全体の中で、工場 \(A_1\) の割合はどのくらいか?を求めているということです。
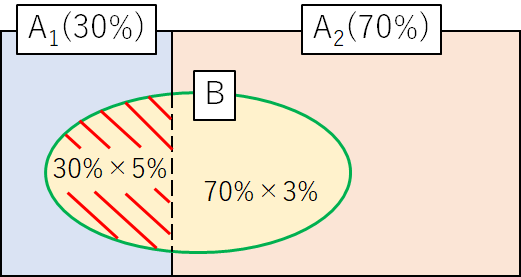
いいかえると、緑で囲った \(B\) の中で、赤色の斜線の割合を求めるのがベイズの定理です。
実際に計算してみると、
\begin{align}
P(A_1|B)&=\frac{P(B|A_1)P(A_1)}{P(B|A_1)P(A_1)+P(B|A_2)P(A_2)}\\
&=\frac{0.05\times 0.3}{0.05 \times 0.3+0.03\times 0.7}\\
&=\frac{5}{12}
\end{align}
となります。
計算式を見ると、ベイズの定理が不良品 \(B\) 全体の中の工場 \(A_1\) の割合をあらわしていることがよく分かります。
記号が多くなると、つい難しいと考えてしまいがちですが、一度立ち止まって図を描いてみるとベイズの定理をよく理解できます。
ベイズの定理をより深く理解するためには、いろいろな問題に触れることが近道です。
以下の記事では、ベイズの定理を使った有名な問題を2つ取り上げています。
2つともベイズの定理を知らないと、まちがえやすいです。
まとめ
本記事では、ベイズの定理の意味と証明を、図を使って解説しました。
ベイズの定理は、
原因→結果の確率から、結果→原因の確率
を求める定理です。
条件つき確率の式から導くことができますが、例題で示したように、
「結果 \(B\) のうち、原因 \(A_1\) の割合を求めている」
と捉えると、イメージで理解することができます。
イメージで理解してベイズの定理を使いこなせるようになりましょう。
ベイズの定理をよく理解するには多くの問題に触れることが一番です。



