はじめに
確率を勉強すると必ず出てくる「独立」と「排反」。
筆者は確率を勉強し直したときに2つの意味の違いが分からずに、かなりの時間を使って調べたり考えたりした記憶があります。
なぜ意味の違いが分かりにくいかと申しますと、言葉の意味(詳しくは下で説明します)が似ているように感じられるからです。
しかし、数学的には独立と排反は全く異なる概念で、意味を取り違えると計算ミスにもつながってしまいます。
この記事では独立と排反の違いについて、具体例や数式を交えながら分かりやすく説明していきます。
独立とは
まずは、独立と排反のそれぞれの意味について簡単に見ていきましょう。
確率統計の分野における独立とは、
1つの事象が、他の事象に影響を与えないこと
と言うことができます。
例えば、棒の長さを2回測定するとき、1回目の測定という事象は、2回目の測定結果に影響を与えません。
1回目に長さを測ることで棒が伸び縮みはしませんので。
このとき、2回の測定は独立であると言います。
【統計】独立とはの記事も参考にしてください。
排反とは
続いて排反についてです。排反とは、
2つの事象が同時に起こらないこと
と言うことができます。
例えば、サイコロを1回投げる試行において、1の目が出るという事象と、3の目が出るという事象は同時に起こりません。
排反の説明はしばしばベン図を使って表現されます。
2つの事象をA、Bとすると排反は下図のように表されます。
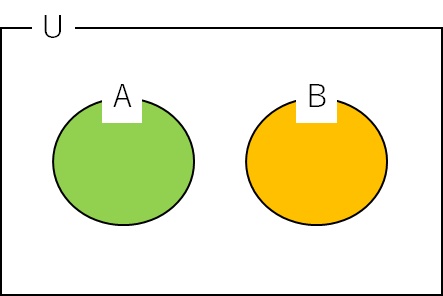
この図のポイントは、AとBに重なっている部分がないということです。
例えば先ほどのサイコロを1回投げるという試行では、
A…1の目が出る事象
B…3の目が出る事象
に相当します。
数式で見る独立と排反の違い
お待たせしました。
独立と排反の準備が整ったところで、これらの違いについて説明していきます。
上で述べたことをおさらいすると、
独立とは、2つの事象が互いに影響を及ぼさないこと
排反とは、2つの事象が同時に起こらないこと
です。言葉で書くと全く同じように見えてしまいますので、次の例題で考えます。
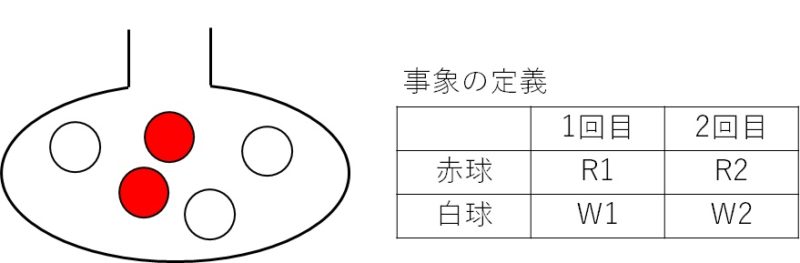
つぼの中に赤球が2個、白球が3個入っている。
このつぼの中から球を1個取り出して色を確認し、元に戻す。
この操作を2回繰り返すとき、独立と排反がどのように式で表されるか。
この問題で独立と排反がどのように違うのかを説明し、数式で表したときの違いについても示します。
上の問題を考えるにあたり、表のように1つ1つの事象に名前をつけます。(RはRed、WはWhiteの意味)
例えば、1回目に赤球を取り出すという事象をR1と書くことにします。
まずは「独立」がどのように表現されるかについてです。
1回目に赤球、2回目に白球を取り出す場合を考えます。
1回目に取り出した球の色は、2回目に白球を取り出す確率に影響を与えないので、1回目と2回目の試行は独立です。
つまり、
$$P(R1 \cap W2) = P(R1) \times P(W2)$$
です。詳しくは【統計】独立とはを参照してください。
続いて排反を式で表してみます。
1回目に赤球、1回目に白球を取り出す場合を考えます。
1回に1個の球しか取り出しませんので、当然、赤球と白球を同時に取り出すことはできません。
つまり、1回目に赤球を取り出すという事象と、1回目に白球を取り出すという事象は排反です。
式で表すと、
$$P(R1 \cap W2) = 0$$
同時に起こる確率は 0 という意味です。
上の式を見て、独立と排反の違いに気づきましたでしょうか。
2つの事象が同時に起こる確率を考えたとき、
独立ならば、それぞれの事象の掛け算で計算することができる
排反ならば、確率は 0 となる
式で見ると一目瞭然です。
つまり、2つの事象が独立か排反かで迷ったら、同時に起こる確率を考えることで早く判断することができます。
まとめ
いかがでしたでしょうか。
独立と排反の言葉の意味と確率をまとめると、
独立
【意味】2つの事象が互いに影響を及ぼさないこと
【同時確率】2つの事象をA1、A2とすると
$$P(A1 \cap A2) = P(A1) \times P(A2)$$
排反
【意味】2つの事象が同時に起こらないこと
【同時確率】2つの事象をB1、B2とすると
$$P(B1 \cap B2) = 0$$
となります。
皆さんの理解の助けとなれば幸いです。


